雙因子變異數分析 (Two Way ANOVA)
套路23: 雙因子變異數分析 (Two Way ANOVA)
應用雙因子變異數分析的資料有二影響因子,就是有兩個自變項。此檢定有三組H0和HA。
H0: m因子1-1 = m因子1-2 = … = m因子1-m,HA: 至少有一組平均值不同。
H0: m因子2-1 = m因子2-2 = … = m因子2-n,HA: 至少有一組平均值不同。
H0: 因子1與因子2互不影響,HA: 因子1與因子2互相影響。
1. 使用時機: 變異數分析適用連續資料之差異分析,若自變項有兩個,就是雙因子變異數分析。
2. 分析類型: 母數分析(parametric analysis)。直接使用資料數值算統計叫parametric方法,把資料排序之後用排序的名次算統計叫non-parametric方法。
3. 假設前提: 每組資料(observations within each cell)都是常態分布(normally distributed)且具相同變異數(equal variances)。
4. 範例資料: 咪路調查人類血漿中鉀離子濃度(mg/100 ml)資料如下:
|
沒注射賀爾蒙
|
注射賀爾蒙
|
||
|
雌
|
雄
|
雌
|
雄
|
|
16.3
|
15.3
|
38.1
|
34.0
|
|
20.4
|
17.4
|
26.2
|
22.8
|
|
12.4
|
10.9
|
32.3
|
27.8
|
|
15.8
|
10.3
|
35.8
|
25.0
|
|
9.5
|
6.7
|
30.2
|
29.3
|
H0: 注射賀爾蒙沒影響。 HA: 注射賀爾蒙有影響。
H0: 性別沒影響。 HA: 性別有影響。
H0: 性別及注射賀爾蒙沒交互作用。 HA: 性別及注射賀爾蒙有交互作用。
第一步: 使用基本模組(base)的read.table函數輸入建立資料儲存到變數m。
m <- read.table(header = TRUE, text = "
Hor Sex Conc
N_H F 16.3
N_H F 20.4
N_H F 12.4
N_H F 15.8
N_H F 9.5
N_H M 15.3
N_H M 17.4
N_H M 10.9
N_H M 10.3
N_H M 6.7
A_H F 38.1
A_H F 26.2
A_H F 32.3
A_H F 35.8
A_H F 30.2
A_H M 34
A_H M 22.8
A_H M 27.8
A_H M 25
A_H M 29.3")
# 資料間以空白間隔,N_H: 沒注射賀爾蒙A_H: 有注射賀爾蒙。
attach(m) # 告知R使用資料m。
names(m)
# 指定資料標題。
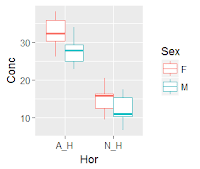
5. 畫圖看資料分佈:
第一步: 安裝程式套件ggplot2。
第二步: 呼叫ggplot2。
library(ggplot2)
第三步: 使用函數ggplot代入m資料畫box圖。
ggplot(m, aes(x = Hor, y
= Conc, color = Sex)) +
geom_boxplot() # 畫box圖
6. 檢查因子間是否有交互作用(interaction):
第一步: 使用基本模組(base)的interaction.plot函數來畫兩個因子交互作用的狀況。
interaction.plot(Sex, Hor,
Conc)
# 兩線有交叉表示有兩因子interaction,兩線平行表示兩因子無interaction,兩線接近平行表示
兩因子interaction很弱。
7. 計算雙因子變異數分析:
第一步: 使用基本模組(base)的aov函數代入m中資料來計算雙因子變異數分析,結果儲存到變數fm。
fm <- aov(Conc ~ Hor
* Sex, data = m)
第二步: 使用基本模組(base)的summary函數代入fm來顯示雙因子變異數分析結果。
summary(fm)
Df Sum Sq Mean Sq F value Pr(>F)
Hor 1 1386.1 1386.1
73.585 2.22e-07 ***
Sex 1 70.3
70.3 3.733 0.0713 .
Hor:Sex 1 4.9
4.9 0.260 0.6170
Residuals 16 301.4
18.8
---
Signif. codes: 0 ‘***’ 0.001
‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# Hor p < 0.05,H0: 注射賀爾蒙沒影響,不成立。
# Sex p > 0.05,H0: 性別沒影響,成立。
# Hor:Sex p > 0.05,H0: 雙因子沒交互作用,成立。
第三步: 使用基本模組(base)的TukeyHSD函數代入fm來計算顯示有差異的組別。
TukeyHSD(fm)
Tukey multiple comparisons of means
95% family-wise
confidence level
Fit: aov(formula = Conc ~ Hor * Sex, data = m)
$Hor
diff lwr
upr p adj
N_H-A_H -16.65 -20.76469 -12.53531 2e-07
$Sex
diff lwr
upr p adj
M-F -3.75 -7.864692 0.3646918 0.0712638
$`Hor:Sex`
diff lwr upr
p adj
N_H:F-A_H:F -17.64 -25.493382
-9.786618 0.0000452 # p < 0.05
A_H:M-A_H:F -4.74
-12.593382 3.113382 0.3428025
N_H:M-A_H:F -20.40 -28.253382 -12.546618 0.0000078 # p
< 0.05
A_H:M-N_H:F 12.90 5.046618
20.753382 0.0012416 # p < 0.05
N_H:M-N_H:F -2.76
-10.613382 5.093382 0.7485244
N_H:M-A_H:M -15.66 -23.513382
-7.806618 0.0001729 # p < 0.05
# p < 0.05是平均值有差異的組別。
8. 檢查不同組別數值是否符合常態分布假設前提(Check the normality assumption)。
第一步: 使用基本模組(base)的residuals函數代入fm來顯示雙因子分析的殘差結果存入變數
aov_residuals。
aov_residuals <-
residuals(object = fm)
第二步: 使用基本模組(base)的shapiro.test函數代入aov_residuals來檢查不同組別數值是否符合常態分布。
shapiro.test(x =
aov_residuals)
Shapiro-Wilk normality test
data: aov_residuals
W = 0.94671, p-value = 0.3198
# p < 0.05不同組別數值不符合常態分布。
# p > 0.05不同組別數值符合常態分布。
9. 檢查不同組別數值是否符合相同變異數假設前提(Check the homogeneity of variance
assumption)。
第一步: 安裝car程式套件。
第二步: 呼叫car程式套件備用。
library(car)
第三步: 閱讀car程式套件leveneTest函數使用說明。
help(leveneTest)
第四步: 使用leveneTest函數檢查不同組別數值是否符合相同變異數。
leveneTest(Conc ~ Hor *
Sex, data = m)
Levene's Test for Homogeneity of Variance (center = median)
Df F value
Pr(>F)
group 3 0.0382 0.9897
16
# p < 0.05不同組別數值不符合相同變異數。
# p > 0.05不同組別數值符合相同變異數。
來勁了嗎? 想知道更多?? 補充資料(連結):
4. 關於R基礎,R繪圖及統計快速入門:
a. R Tutorial: https://www.tutorialspoint.com/r/index.htm
b. Cookbook for R: http://www.cookbook-r.com/
c. Quick-R: https://www.statmethods.net/
d. Statistical tools
for high-throughput data analysis (STHDA): http://www.sthda.com/english/
e. The Handbook of Biological Statistics: http://www.biostathandbook.com/
f. An R Companion for the Handbook of
Biological Statistics: http://rcompanion.org/rcompanion/index.html
5. Zar, JH. 2010. Biostatistical Analysis, Fifth Edition,
Pearson.

留言
張貼留言