比較兩組直線回歸方程式 (Comparing Two Simple Linear Regression Equations)

套路42: 比較兩組直線回歸方程式
(Comparing Two Simple Linear Regression Equations)

1. 使用時機: 比較兩組直線回歸方程式統計上是否有顯著差異。
2. 分析類型: 母數分析(parametric analysis)。
3. 範例資料: 咪路測量兩組動物體溫(°C)與脈搏，資料如下：
體溫1
20.8
20.8
24
24
24
24
26.2
26.2
26.2
26.2
28.4
29
30.4
30.4
脈搏1
67.9
65.1
77.3
78.7
79.4
80.4
85.8
86.6
87.5
89.1
92.6
94.8
96.3
99.7
體溫2
17.2
18.3
18.3
18.9
18.9
20.4
21
21
22.1
23.5
24.2
25.9
26.5
29.6
脈搏2
44.3
47.2
47.6
49.6
50.3
51.8
56.5
58.9
60
63.7
69.8
72.9
77
84
4. 輸入建立資料:
第一步: 使用基本模組(base)的read.table函數輸入建立資料儲存到變數dat中。
dat <- read.table(header = T, text = "
Species Temp Pulse
ex 20.8 67.9
ex 20.8 65.1
ex 24 77.3
ex 24 78.7
ex 24 79.4
ex 24 80.4
ex 26.2 85.8
ex 26.2 86.6
ex 26.2 87.5
ex 26.2 89.1
ex 28.4 92.6
ex 29 94.8
ex 30.4 96.3
ex 30.4 99.7
niv 17.2 44.3
niv 18.3 47.2
niv 18.3 47.6
niv 18.9 49.6
niv 18.9 50.3
niv 20.4 51.8
niv 21 56.5
niv 21 58.9
niv 22.1 60
niv 23.5 63.7
niv 24.2 69.8
niv 25.9 72.9
niv 26.5 77
niv 29.6 84")  # Species、Temp及Pulse資料以空白分隔。
第二步: 使用基本模組(base)的attach及names函數賦予dat中的資料名稱(標題)。
  attach(dat)  # 讓R能透過變數名稱搜尋資料。
  names(dat)  # 賦予資料名稱(標題)。

5. 畫圖看資料分佈:
第一步: 安裝ggplot2程式套件。
第二步: 呼叫ggplot2備用。
  library(ggplot2)
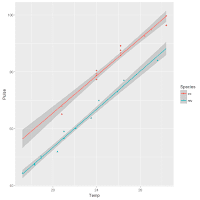
第三步: 使用ggplot2程式套件的函數ggplot代入dat資料畫x-y散佈圖及回歸線。
  ggplot(dat, aes(x = Temp, y = Pulse, color = Species, shape = Species)) +
    geom_point() +   # x-y散佈圖
    geom_smooth(method = lm, fullrange = TRUE)  # 畫回歸線，及95%信賴區間。
# 灰色區域為95%信賴區間。
6. 使用R比較兩回歸方程式統計上是否有差別:
第一步: 安裝car程式套件。
第二步: 呼叫car備用。
  library(car)
第三步: 使用基本模組(base)的lm函數計算回歸模型1。
  model1 <- lm(Pulse ~ Temp * Species, data = dat)
第四步: 使用car程式套件的Anova函數計算並顯示結果。
  Anova(model1, type = "II")
第五步: 判讀model1結果。
Anova Table (Type II tests)
Response: Pulse
                 Sum Sq Df   F value    Pr(>F)   
Temp         3275.6  1 1165.5187 < 2.2e-16 ***
Species       719.9  1  256.1441 2.625e-14 ***
Temp:Species    0.4  1    0.1538    0.6984   
Residuals      67.5 24                       
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
  # H0: b1 = b2，HA: b1 ≠ b2。
  # Temp:Species項Pr < 0.05，H0: b1 = b2不成立。
  # Temp:Species項Pr > 0.05，H0: b1 = b2成立。
第六步: 使用基本模組(base)的lm函數計算回歸模型2。
  model2 <- lm(Pulse ~ Temp + Species, data = dat)
第七步: 使用car程式套件的Anova函數計算並顯示結果。
  Anova(model2, type = "II")
第八步: 判讀model2結果。
Anova Table (Type II tests)
Response: Pulse
          Sum Sq Df F value    Pr(>F)   
Temp      3275.6  1 1206.35 < 2.2e-16 ***
Species    719.9  1  265.12 8.105e-15 ***
Residuals   67.9 25                     
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
  # H0: 兩條線截距(elevation)相同，HA: 兩條線截距(elevation)不相同。
  # 類別變數(Species)項Pr < 0.05，H0: 兩條線截距(elevation)相同，不成立。
  # 類別變數(Species)項Pr > 0.05，H0: 兩條線截距(elevation)相同，成立。

來勁了嗎? 想知道更多?? 補充資料(連結):
1. 關於Simple linear regression (https://en.wikipedia.org/wiki/Simple_linear_regression)
2. 關於Linear regression (https://en.wikipedia.org/wiki/Linear_regression)
3. STHDA Linear Regression Essentials in R (http://www.sthda.com/english/articles/40-regression-analysis/165-linear-regression-essentials-in-r/)
4. 關於R基礎，R繪圖及統計快速入門:
   a. R Tutorial: https://www.tutorialspoint.com/r/index.htm
   b. Cookbook for R: http://www.cookbook-r.com/
   c. Quick-R: https://www.statmethods.net/
   d. Statistical tools for high-throughput data analysis (STHDA): http://www.sthda.com/english/
e. The Handbook of Biological Statistics: http://www.biostathandbook.com/
f. An R Companion for the Handbook of Biological Statistics: http://rcompanion.org/rcompanion/index.html
5. Zar, JH. 2010. Biostatistical Analysis, Fifth Edition, Pearson.

留言

張貼留言

這個網誌中的熱門文章

統計不球人 目錄 (Table of Contents)

用 R 做生醫資料科學   (Biomedical Data Science using R) 如何選擇統計方法 1 如何選擇統計方法  2 ***************************   第一段 : 起手式   ****************************** 套路 0: 安裝 R 不球人 套路 1: R 算統計不球人 ， 使用 R 函數 套路 2: 使用 ggplot2 繪圖 (Graphics using ggplot2) 套路 3: 敘述性統計 (Descriptive Statistics) 套路 4: 如何檢查資料是否接近常態分布 (Check Normality using R) 套路 5: 機率分布 (Probability Distributions) ***************************   第二段 : 比較平均值、中數   *************************** 套路 6: 單一樣本 Z 檢定 (One-Sample Z test) 套路 7: 單一樣本 t 檢定 (One-Sample t test) 套路 8: 單一樣本 Wilcoxon signed-rank 檢定 ( One-Sample Wilcoxon signed-rank test ， non-parametric ) 套路 9: 單一樣本符號檢定 (One Sample Sign test) 套路 10: 兩組獨立樣本 Z 檢定 (Two-Sample Z Test) 套路 11: 兩組變異數相同獨立樣本 t 檢定 ( t Test for Two-Samples with Equal Variances) 套路 12: 兩組變異數不同樣本 t 檢定 ( t Test for Two-Samples with Unequal Variances ， Welch Two Sample t test) 套路 13: 成對樣本 t 檢定 (Paired Sample t test) 套路 14: 兩組獨立樣本曼恩 - 惠尼 U 檢定 (...
閱讀完整內容

如何選擇統計方法 1

如何選擇統計方法 1 第一步 : 選擇統計方法可 依照統計方法用途的分類 來選擇統計方法 。 第二步 : 要了解確認統計方法的用途可看他的虛無假設 (Null hypothesis) H 0 。 以下為統計方法用途分類及本站網頁聯結 。 類別 1. 對資料進行基本分析 ， 以了解資料的大概情況 (summary) ， 例如平均值 、 中位數 、 四分位數 、 有無離群值 (outlier) 及是否為常態分布等 … 敘述性統計 (Descriptive Statistics) 如何檢查資料是否接近常態分布 (Normality Test using R) 類別 2. 比較平均值 (mean) 或中位數 (median) 2.1. 單一樣本 ( 與期望值或特定值相比 ) 單一樣本 Z 檢定 (One-Sample Z test) 單一樣本 t 檢定 (One-Sample t test) 單一樣本 Wilcoxon signed-rank 檢定 ( One-Sample Wilcoxon signed-rank test) 單一樣本符號檢定 (One Sample Sign test) 2.2. 兩組獨立樣本 ( 兩組獨立樣本相比 ) 兩組獨立樣本 Z 檢定 (Two-Sample Z Test) 兩組變異數相同樣本 t 檢定 (t Test for Two-Samples with Equal Variances) 兩組變異數不同樣本 t 檢定 (t Test for Two-Samples with Unequal Variances ， Welch Two Sample t-test) 兩組獨立樣本曼恩 - 惠尼 U 檢定 (Two-Sample Mann-Whitney U Test) 比較兩組獨立次序資料 (Two-Sample Test for Ordinal Data) 兩組獨立樣本 Mood's 中位數檢定 (Two-Sample Mood's Median Test) 2.3. 兩組成對樣本 ( 兩組成對樣本相比 ) 成對樣本 t 檢定 (Pai...
閱讀完整內容

單因子多樣本中位數差異檢定 (Kruskal-Wallis test)

圖片
套路 21: 單因子多樣本中位數差異檢定 (Kruskal-Wallis test) 變異數分析適用連續資料之差異分析，若自變項有一個，就是單因子變異數分析。 多樣本中位數差異檢定是對應 單因子變異數分析的無母數分析方法。當數據不符合單因子變異數分析的前提假設 ( 相同變異數，數據為常態分布 ) 時，可選擇 多樣本中位數差異檢定來做為替代分析方法 。 ** 注意 ** ” 比較變異數 ” (comparing variances) 和 ” 變異數分析 ” (analysis of variance) 不同。變異數分析是多組資料比較平均值或中位數。統計假設檢定檢定什麼 ? 看 H 0 。例如多組獨立樣本假設檢定 H 0 : k 組樣本中位數相同， H A : 至少有一組中位數不同 ， 是檢定多組資料的中位數是否相同。假設相等時為雙尾 (two-tailed test) 檢定。 1. 使用時機 : 用於比較多組樣本中位數 (median) 。 2. 分析類型 : 無母數分析 (non-parametric analysis) 。 直接使用資料數值算統計叫 parametric 方法，把資料排序之後用排序的名次算統計叫 non-parametric 方法。 3. 假設前提 : 無。 4. 範例資料 : 咪路調查餵食不同飼料的肉雞體重 (g) ， 資料如下： 飼料 1 飼料 2 飼料 3 飼料 4 61.8 78.8 70.5 60.3 65.1 79.5 72.6 63.8 61.7 76.0 71.7 64.1 63.3 73.4 72.0 61.4 77.3 71.1 60.9 不同飼料是否效果不同 ? H 0 : 餵食不同飼料的肉雞體重 ( 中位數 ) 相同。 H A : 餵食不同飼料的肉雞體重 ...
閱讀完整內容